| Pages:
1
..
8
9
10
11
12
..
16 |
patheslip
Oud Junkie
    
Posts: 160
Registered: 5-24-2008
Location: Welsh Marches
Member Is Offline
Mood: smooth
|
|
I know less than nothing about acoustics, but I'm enjoying your postings nevertheless. I especially like your tying together of theory and
experiment; Friar Bacon would be proud of you.
I wonder what the effects of a rose are on the sounds, both in terms of resonant frequency and of filtering out some notes. I though these could
include dampening down of high frequency squeaks and plectrum sound, but the size of the spacing between the parts of the rose is measured in
millimetres. This would give frequencies of well above hearing: bat level. . So
perhaps I'm talking nonsense. . So
perhaps I'm talking nonsense.
|
|
|
jdowning
Oud Junkie
    
Posts: 3485
Registered: 8-2-2006
Location: Ontario, Canada
Member Is Offline
Mood: No Mood
|
|
Thanks for your comments patheslip.
I am wondering the same thing about sound holes with rosettes and will be attempting to explore that question first of all theoretically and then on
the 'test bed' of the project oud once completed. I also know little about acoustics so I am feeling my way through this investigation - and hopefully
learning something useful in the process. So, if I miscalculate or make any missteps along the way feel free to comment!
As well, I am not sure about how multiple sound holes should be treated so my first step with the project oud design will be to undertake calculations
based on a single open sound hole (ie following the Arnault de Zwolle geometry) and then to undertake the same exercise with a rosette in place. I
have already determined the open space area of the 'Gerle' rosette used in this project. The question is should I take this area and assume a smaller
equivalent sound hole diameter for the Helmholtz resonator calculation or should I calculate on the basis of a multitude of small vents that make up
the rosette? I shall of course try to investigate both possibilities. Just to complicate matters, sound holes that are not circular do not have an
equal end effect as a circular sound hole of the same area.
For information and for the record here is the data used in calculating the resonant frequency of the guitar.
Total volume of the body, V = 12,957 cubic centimeters.
Diameter of sound hole = 8.7 centimeters, radius (r) = 4.35 cm.
Sound hole area, A = 59.45 square centimeters.
Speed of Sound at 20C, c = 34,300 centimeters per second
Effective L = L (measured) + 0.85r + 0.85r = 1.7x4.35 = 7.4 cm
L (measured) is only a mm or so and can be ignored. There is a double end effect - inside and outside the sound board.
These figures give a calculated resonant frequency of 136 Hz due to the guitar being a less than perfect Helmholz resonator (an overestimate due to
the flexible body 'ballooning' under pressure, high internal resistance etc). Had the guitar been a perfect Helmholtz resonator the sound hole
diameter would have had to have been 5.7 cm compared to 8.7 cm actual in order to resonate at 110 Hz.
Therefore, the actual sound hole diameter of the guitar has been made 53% larger than that predicted by theory.
The radius of a sphere of volume 12,957 c.c. is 14.57 cm. so the ratio of sound hole diameter to diameter of the sphere is 0.298 say, 0.3 - which is
within the optimum design range of the resonators used by Helmholtz in his experiments.
So, the next step is to move on to examine the geometry of oud of this project.
|
|
|
jdowning
Oud Junkie
    
Posts: 3485
Registered: 8-2-2006
Location: Ontario, Canada
Member Is Offline
Mood: No Mood
|
|
Turning to the oud, the first step is to determine the volume of the bowl. As the bowl is complete and the sound board yet to be glued in place, a
direct volumetric measurement was possible using granular solids. I used cracked corn but rice or wheat grains or fine sawdust would do just as well.
The volume of grain was carefully measured using a kitchen 1 litre measure, the bowl being filled to the brim. Using this method the bowl volume was
measured as exactly 12,000 cubic centimeters.
A second method used was to divide the bowl template into
1 cm wide segments, measure the mean radius of each segment and calculate the volume of each one which for this instrument is semicircular in cross
section (see attached image). Adding the volume of all segments gave a total calculated volume of 12,360 cubic centimeters.
This method over estimates the volume because the bowl section is not a smooth semicircle but is made from wide ribs and so facetted like a lute. Also
the calculation takes no account of the thickness of the interior rib reinforcement strips.
The difference of 360 c.c. is equivalent to an evenly spread thickness of about 1.5 mm on the interior surface area of the bowl. (The interior surface
area was calculated by measuring the area of the rib pattern and multiplying by 11). This seems reasonable.
Therefore a volume of 12,000 c.c. for the bowl will be taken as close enough.

|
|
|
patheslip
Oud Junkie
    
Posts: 160
Registered: 5-24-2008
Location: Welsh Marches
Member Is Offline
Mood: smooth
|
|
I wonder if you could simplify the 'rose' question by using a spherical resonator, perhaps a piece of glass lab equipment would be sufficiently hard
and smooth. I seem to remember for my long-ago Chemistry that there were glass vessels with necks and round bodies.
|
|
|
jdowning
Oud Junkie
    
Posts: 3485
Registered: 8-2-2006
Location: Ontario, Canada
Member Is Offline
Mood: No Mood
|
|
Glass laboratory retort receivers were used by Helmholtz (presumably modified a bit - neck length) for his initial experiments with resonators but his
'custom made' glass resonators were rather more substantial in wall thickness to eliminate any possibility of flexing of the walls of the sphere -
very important as it affects the spring constant of the contained air inside the sphere. If the walls can flex (as they surely can in a musical
instrument) then, the 'spring effect' of the contained air is 'softened' which results in an over estimate of the calculated resonant frequency.
On further thought, I may be able to use the guitar to try to test out the rosette question using a card perforated with holes of precise dimension to
cover the sound hole.
However, it may well be that the complexity of an oud or lute rosette may invalidate use of the Helmholz resonator equation in usefully predicting the
Helmholtz resonance of an oud or lute bowl. We will see.
The single sound hole diameter of the project oud (ie according to Arnault de Zwolle) - taken from the full scale geometrical layout - is 10.4 cm.
This gives a Helmholtz resonant frequency of 154 Hz.
This, we know, is an overestimate but without a completed instrument to test, we do not know by how much. For the guitar, the over estimate was 24%. I
would expect an oud bowl to be stiffer than a guitar body so - making a wild guess - might be, say, a 20% overestimate. which would give an actual
resonant frequency of around 123Hz or about the tone B (at A440). The significance of this result has yet to be determined!
For information, the sound hole diameter to resonator sphere diameter is 0.37, again, within the range of ratios of the resonators employed by
Helmholtz.
Now to take a closer look at the rosette (shamsa) question.
|
|
|
jdowning
Oud Junkie
    
Posts: 3485
Registered: 8-2-2006
Location: Ontario, Canada
Member Is Offline
Mood: No Mood
|
|
The first question is - does an instrument with a complex rose pattern, like a traditional oud or lute, act as a Helmholtz resonator in the same way
as, for example, a classical acoustic guitar with an open sound hole?
I currently have two functional lutes - a copy of a seven course late 16th C lute by Giovanni Hieber and a reconstruction of an early six course 16th
c lute by Laux Maler. These were both tested - like the classical guitar in this project - by sliding a card over the rose while sounding each course.
Both instruments responded most loudly when the sound hole was fully uncovered (as in the guitar tests) when the 5th course was sounded. The Hieber
lute is tuned in 'g' so the Helmholtz resonance in this case is 'c' and the Maler lute is tuned in 'd' so the resonance is 'g' - i.e. at concert pitch
A440.
The lute makers of the 16th C to 17th C seemed to have understood the relationship of sound hole diameter to bowl volume as it affects bass response
as the evidence suggests that they adjusted the sound hole diameters accordingly.
Lute rosette patterns were standardised so the luthiers - if they required a smaller or larger sound hole area would either cut only part of a
pattern or would add an additional ring of holes to increase the area - dependent (presumably) on the relationship of sound hole diameter to bowl
volume giving maximum bass response.
For example the first image shows a standard 16th C rose pattern in its basic form, expanded with an additional ring of holes and reduced in area by
cutting only part of the pattern.
The second image shows another pattern (the 'Gerle' rosette subject of this project). Some larger lutes used this pattern, increased in diameter with
an additional ring of holes, (e.g. on a great octave bass lute by Michelle Harton, 1602) or smaller in diameter by using only part of the pattern
(e.g. Martin Hoffmann, 1692).


|
|
|
jdowning
Oud Junkie
    
Posts: 3485
Registered: 8-2-2006
Location: Ontario, Canada
Member Is Offline
Mood: No Mood
|
|
The rosette pattern chosen for this project (often used by many luthiers of the 16th and 17th C) is called here the 'Gerle' pattern.
The first step in the analysis is to break down the rosette into its basic design elements and to measure the open area of each element.
As all of my historical rosettes were originally traced on transparent paper, the 'Gerle' pattern was placed on a mm squared paper background, scanned
and then enlarged.
The area of each element in the design was then measured by counting the squares.

|
|
|
jdowning
Oud Junkie
    
Posts: 3485
Registered: 8-2-2006
Location: Ontario, Canada
Member Is Offline
Mood: No Mood
|
|
The data obtained from measurement of the rosette is as follows:
Diameter of rosette = 9.7 cm (equivalent to an open sound hole area of 74 sq. cm.).
Number of basic elements (holes) of the same size and geometry = 11
Total number of holes in the rosette = 127
Total area of holes = 2150 sq. mm. or 21.5 sq. cm.
Therefore, the total open area of the rosette compared to that of the open area of a sound hole of equal diameter = 21.5/74 = 0.29 or 29% of an open
sound hole.
The tests on my two lutes suggests that the presence of a rosette may not significantly affect the relative Helmholtz resonance phenomenon compared to
that of an instrument with an open sound hole - the lutes and guitar resonating most strongly when the 5th string of each instrument is plucked.
So, does the presence of a rosette make any difference - and if not, why?
|
|
|
freya
Oud Junkie
    
Posts: 276
Registered: 2-8-2004
Location: Asheville NC
Member Is Offline
Mood: Happy in the mountains of WNC
|
|
I recall posting this article some time back but couldn't find it with a quick search. I provide it for reflection only as, typically, no "cookbook"
type formula is given. In any case, it appears that the classical Helmholtz formula will not accurately predict the resonant frequencies of a
hemisphere bounded by a plane with a central opening except under special conditions. It also notes additional properties of non-circular openings.
Perhaps someone more mathematically inclined than I would reformulate the central equation (14) in simple physical terms.
|
|
|
jdowning
Oud Junkie
    
Posts: 3485
Registered: 8-2-2006
Location: Ontario, Canada
Member Is Offline
Mood: No Mood
|
|
Thank you freya.
It would, of course, be too much to expect the Helmholtz formula to accurately predict the resonant frequency of a resonator as complex as a guitar,
oud or lute. The theoretical analyses must inevitably oversimplify the mathematical model - as the Bericht paper does, for example, to a basic, non
flexible, hemisphere with a hole in the plane surface. Nevertheless, I would agree that these investigations do provide food for thought and might
lead to a better understanding of the problem. I can't help with the question about equation 14 though!
Not to worry - the ancient luthiers who likely had a greater detailed understanding of instrument acoustics (i.e. what makes a 'good' instrument for
their time period) than we might dare to imagine today, most likely acquired this knowledge by 'hands on' trial and error. The lute makers (and the
oud makers) most likely did have some 'rule of thumb' that dictated optimum sound hole diameter to bowl volume to give a particular cavity resonance
for a given instrument tuning.
The earliest recorded evidence of this might be the Arnault de Zwolle lute (with single central sound hole) that is currently under consideration
here. The sound hole diameter is 1/3 of the width of the bowl at the sound hole position so the diameter is proportionally related to the volume. Does
this geometry give optimum resonance for a given tuning? Impossible to say without constructing an instrument as a test bed. So - it looks as though I
must now make a second sound board with single sound hole to investigate! No problem - the results might be of interest!
In the meantime, to further test the question of open sound holes v.s. rosette sound holes, an experimental rosette has been made for my classical
guitar. More to follow.
|
|
|
jdowning
Oud Junkie
    
Posts: 3485
Registered: 8-2-2006
Location: Ontario, Canada
Member Is Offline
Mood: No Mood
|
|
I am using my classical guitar as a test bed - to learn more about the resonance phenomena - with an open sound hole compared to resonance with a
rosette or reduced sound hole diameter. Although a guitar is being used, I would expect ouds or lutes to provide similar results.
In an attempt to quantify the results for comparative purposes, a reasonable quality digital recorder (Zoom H2) - positioned directly over the sound
hole - has been used to record the sound for each test and the recordings analysed using Audacity - the free audio editor.
Test 1
A 3 mm thick card was used to seal the sound hole closed and - after sounding the 5th (A) string - was quickly slid to fully open the sound hole. At
the point where the soundhole was completely uncovered, the sound volume suddenly increased with a definite pressure pulse. Repeating the procedure
for the 6th (E) string, there was a similar sound pulse at the point where the sound hole was uncovered by about a third.
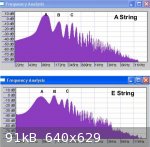
The first image (stereo channels) shows the 'loudness response' with the A string sounded - X being the point when the soundhole is fully
uncovered.
The second image shows the same response with the E string sounded - X being the point when the soundhole is partially uncovered.
The last image shows the frequency response analysis for the A and E strings sounded.
The peak loudness points for the A string graph are A = 111Hz A2, B = 217Hz A3 and C = 435Hz A4.
For the E string graph, A = 81Hz E2, B = 161Hz E3 and C = 328Hz E4.
A couple of sound clips are also attached to illustrate the sound pulse that can be distinctly heard when the (Helmholtz) resonant frequency of the
enclosed volume of air in the guitar body occurs.
All a bit' rough and ready' at the present time as I learn how to use the hardware and software and interpret the results - to try to understand what
it all means!
[file]11480[/file]
[file]11482[/file]
[file]11483[/file]

|
|
|
jdowning
Oud Junkie
    
Posts: 3485
Registered: 8-2-2006
Location: Ontario, Canada
Member Is Offline
Mood: No Mood
|
|
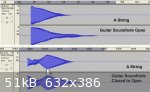
The attached images show the experimental set up to test the Helmholtz resonances with the A and then the E string sounding.
All a bit rough and ready - just to get a feel for the possibilities. The guitar back is resting on a carpeted floor. The Zoom H2 digital recorder is
positioned directly over the sound hole mounted on a camera tripod. The recorder has four microphones - two facing forward and two facing rearward. So
that the digital display could be read during the test, the two rear facing microphones were used to record sound - aligned along the centre-line of
the guitar sound board (for convenience).
The first image shows the start position of the card - completely covering the sound hole.
The second image shows the position of the card that gave maximum sound amplitude with the E string sounding (about a third uncovered) and the last
image shows the position of the card that gave maximum sound amplitude with the A string sounding (fully uncovered).
The waveforms and frequency analysis charts previously posted confirm that the sound hole to body volume geometry accentuates the sound volume of the
two bass strings using the Helmholtz resonance effect.
With the recorder placed in this position, the right microphone (facing the finger board) records a lower sound volume than the left microphone
(facing the bridge). The recorder will, therefore, be re-oriented for repeat testing to minimise this effect.
I am also surprised to find that the sustain of the A string - given by the waveform - is only about 5 seconds, possibly because I may have exerted
some pressure on the card in the fully withdrawn position thus restricting the free vibration of the sound board (?).
All to be re-checked with further tests.

|
|
|
jdowning
Oud Junkie
    
Posts: 3485
Registered: 8-2-2006
Location: Ontario, Canada
Member Is Offline
Mood: No Mood
|
|
The second trial will investigate what happens when the guitar sound hole is covered with a rosette with an open hole area, relative to the open sound
hole area of the guitar, of 0.29.
To save time, the test rosette has been made from 1mm thick card accurately pierced with holes of precise diameter using a tinsmiths hole punch. A
preliminary test with the rosette taped in place gave similar results to those of Test 1 except that the sound volume at resonance was slightly
reduced and the sustain of the A string was much greater. However, as the card has some flexibility, the test will be repeated with the rosette
reinforced with small cross braces and with the rosette taped in position all around its circumference.
The third test will be to reduce the guitar sound hole diameter so that its area - like that of the rosette - is 0.29 of the full sound hole area.
Preliminary tests indicate that the Helmholtz response is minimised (almost eliminated) with the A string sounding and maximised with the E string
sounding - which is what might be expected. However, this test will be run again with the inside edge of the card sound hole reinforced to reduce any
flexibility and the card fully taped in position like the rosette.

|
|
|
jdowning
Oud Junkie
    
Posts: 3485
Registered: 8-2-2006
Location: Ontario, Canada
Member Is Offline
Mood: No Mood
|
|
The small sound hole and rosette test cards have been reinforced and coated with a hard 'spar' varnish ready for a trial re-run.
The digital recorder was positioned as before but tilted to try to reduce the difference in recorded sound amplitude between the left and right
microphones.
Ideally, a special rig should be contrived to ensure a consistent plucking force on the strings. However, with a little practice, reasonable
consistency was achieved without need for special equipment. The strings were plucked with fingertips not finger nails.
Using "Audacity" freeware audio editing software, the waveforms were produced from the recorded sound tracks for comparison - the horizontal axis
measured in seconds and the vertical axis in decibels (a logarithmic measure of sound level or sound intensity). The waveforms were 'photographed' to
image file using screen capturing software (freeware MWSnap)
Re-Test 1. The response with guitar sound hole uncovered and then when sliding a card from fully covered to open was recorded with first the A and
then the E string sounding.
The sliding card action produced a sound pulse when the sound hole was fully uncovered with the A string sounding and when the sound hole was about a
third uncovered with the E string sounding (points X on the waveform graphs) - confirming the results previously posted. The pulses are the Helmholz
resonances for frequency A and E.
The recorded maximum sound duration of the waveforms is only about 5 seconds yet the sound of the string vibration could be heard for about 15
seconds.
Comparative test results for the rosette and small sound hole are to follow.


|
|
|
shayrgob
Oud Maniac
   
Posts: 57
Registered: 9-23-2009
Location: Chi-Town!
Member Is Offline
Mood: No Mood
|
|
Jdowning: What do you do for a living?? I'm fascinated by this but it's a little beyond me.
|
|
|
jdowning
Oud Junkie
    
Posts: 3485
Registered: 8-2-2006
Location: Ontario, Canada
Member Is Offline
Mood: No Mood
|
|
I am also at present trying to understand what is going on shayrgob - so you are in good company. Now retired from the workforce, my training as a
professional engineer did not include instrument acoustics.
Hopefully the data collected here will eventually be of some use at a later date.
A little surprised by the brief sustain of the recorded waveform (perhaps because the sound samples were recorded at lowest sound levels?), I ran a
test to check the sustain of the guitar using my own hearing as judge. The sustain in each case, measured with a stop watch, was about 16 seconds for
the open sound hole, rosette and small sound hole - no difference between them. With the guitar sound hole sealed with 3mm thick card taped in place,
the measured sustain was about 14 seconds. I conclude from this that the guitar might work quite well acoustically if it had no sound hole at all!
Test 2. Rosette taped in place and sound recordings made first with the rosette open and then from closed to open (as in Trial 1) sounding first the A
and then the E strings.
The attached images show the waveforms.
It is interesting to note that, compared to the guitar open sound hole tested in Test 1, the duration of the waveform for the A string is almost
doubled with a much smoother attenuation (i.e. reduction in amplitude with time of the waveform) from the maximum sound levels.
On the other hand, the E string waveforms in Test 1 and 2 are comparable.
Test 3 with the small sound hole to follow.


|
|
|
jdowning
Oud Junkie
    
Posts: 3485
Registered: 8-2-2006
Location: Ontario, Canada
Member Is Offline
Mood: No Mood
|
|
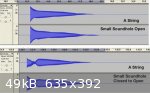
Test 3. The small sound hole is 29% of the area of the guitar sound hole (and has the same open area as the rosette).
As anticipated, the smaller sound hole area moves the Helmholtz effect pressure pulse to tone E - almost, but not quite, as a small pulse can still be
seen in the waveform of the A string.
Note also that the attenuation of waveform is about 6.5 seconds compared to about 5 seconds for the open guitar sound hole.
The difference between the rosette and the small sound hole waveforms with the A string sounding - both of equal open area - is distinctive.
Note that when comparing the waveforms, the scale of the horizontal time line can vary. The sound amplitude in Decibels is consistent between
files.
Out of curiosity, an additional test 4 with a sound hole area of only 16 % of the guitar sound hole will be tried next - to see if the Helmholtz
resonant effect will be moved further away from both A and E tones.

|
|
|
jdowning
Oud Junkie
    
Posts: 3485
Registered: 8-2-2006
Location: Ontario, Canada
Member Is Offline
Mood: No Mood
|
|
I should have noted that in test 3 (with a 49 mm diameter sound hole) when the Helmholtz resonance effect shifted to E as expected, the A string
waveform shows a pressure pulse but this was inaudible.
Test 4 - the sound hole diameter is reduced to 35 mm from the full sized guitar sound hole diameter of 87 mm.
As expected, this shifted the Helmholz resonance effect to a lower tone than A or E although a small (but inaudible) pressure pulse can still be seen
in each of the waveforms.
The overall sustain of both strings increased to about 20 seconds.
It might concluded from these tests that there may be some latitude in sound hole diameters that will work to produce a specified resonance tone. This
may be due to the fact that a guitar (or lute or oud for that matter) is a much less than perfect Helmholtz resonator so that the resonant pitch is
less critically focussed than it would be if using a rigid walled spherical resonator.
The waveforms for the rosette - with only 29% of open sound hole area of the guitar - show the same sound pressure pulses at almost the same sound
amplitude as that of the guitar sound hole. Interestingly, In the case of the A string waveform, the sustain is almost doubled with a smoother
attenuation.
The rosette is essentially a multitude of small sound holes - each (possibly?) with a much longer end correction than the open sound hole of the
guitar - so the cumulative effect may add up to be equal to that of the guitar sound hole.
The sound pulse in the case of the guitar may be quickly dispersed (attenuated) whereas it would take a longer period of time for this to happen with
a rosette? Just guessing at this point in time, however.
Now that I have become more familiar with using the Zoom H2 digital recorder and the Audacity audio editing software, my previous concerns about the
sensitivity of the equipment for recording sound were unfounded.
In fact, the audio fidelity of the recorder is very good so that the full sustain of the guitar over time could be clearly heard and measured by
listening to the sound tracks played back through the stereo headphones of the recorder.
The Audacity software also does a good job in accurately measuring and indicating the sustain duration in the sound volume bar for each recorded
channel - although, of course, the full sustain could not be heard through my low quality computer speakers. The sound amplitude, presented in the
recorded waveforms, is somewhat limited so that after the first burst of sound lasting a few seconds the continuing sound wave cannot be easily
distinguished without considerably magnifying the scale of the waveform.
A neat feature of the software is the frequency analysis facility which allows a small section of the waveform to be highlighted and the peak
frequencies against volume in decibels in the measured sound displayed as a graph. Moving a cursor along the graph displays the peak frequencies and
equivalent tones (C2, G5 etc.) as well as the frequency at the cursor position.
This concludes the sound hole/"Helmholtz resonance" tests for this unplanned interlude diversion in the thread but further tests will be continued
once the project oud is completed.
To this end, I plan to build a second soundboard with the same bracing as the first but with four sound holes - designed to sealed closed or left
open, fitted with reduced diameter sound holes, with or without rosettes etc. Various sound hole combinations may then be subject to testing - all in
the interests of science!


|
|
|
jdowning
Oud Junkie
    
Posts: 3485
Registered: 8-2-2006
Location: Ontario, Canada
Member Is Offline
Mood: No Mood
|
|
Curious about why the test guitar with 'rosette' is little different from the guitar with open sound hole - as far as the Helmholtz resonant frequency
effect of the instrument is concerned - and in an effort to try to understand and explain what is going on, I have made a few calculations (and
assumptions valid or otherwise!). In doing so. I have referred to some interesting and, hopefully, relevant work by others on organ flue pipes -
another kind of resonator
I do not have a 'scientific keyboard' so have scanned my notes, first of all exploring the question of 'end correction' - attached for information.
Precise calculation of the Helmholtz resonant effect of a guitar, oud or lute etc. will, no doubt, defy exact mathematical analysis so any assumptions
made here will, 'at the end of the day', have to be verified by experiment.
To follow - applying the results of the guitar tests to the project oud with 3 sound holes in order to estimate (a.k.a. guess!) the Helmholtz resonant
frequency.
[file]11768[/file]
|
|
|
jdowning
Oud Junkie
    
Posts: 3485
Registered: 8-2-2006
Location: Ontario, Canada
Member Is Offline
Mood: No Mood
|
|
I thought that it would also be an interesting exercise to try to predict the Helmholtz resonant frequency of the project oud - based on the guitar
test findings - applied to three sound holes. The assumptions made here may or may not be valid so will have to be confirmed by experiment on the
completed instrument.
The first assumption is that the formula for a Helmholtz spherical resonator - giving the resonant frequency - will also be approximately true,
proportionally, for musical instruments as resonators. The constant factor - determined by experimentation on real instruments - would probably be
different for each type of instrument.
The second assumption is that the formula will hold true for any number of sound holes by considering each sound hole separately and adding the
individual Area/ End Correction (A/Le) calculations in the Helmholtz resonant formula.
The third assumption - suggested by the guitar tests - is that a sound hole with a rosette can be treated as an open sound hole of the overall
diameter of the rosette. This greatly simplifies the calculation of resonant frequency.
Assuming a K factor of 1 for the project oud gives a resonant frequency of 203 Hz or about G3 (if I have done the sums correctly).
This will be an over estimate - judging from the guitar tests - where the calculated resonant frequency of the guitar is
136 Hz when it should have been 110 Hz (A440 pitch) - i.e. about 24% overestimate. This gives a K factor for the guitar of 0.81.
The K factor for the oud may be a bit less than this - the bowl of the oud being a stiffer structure than the guitar. Guessing a 20% overestimate of
resonant frequency for the oud (and it is just a guess a this point in time) would give a K factor of about 0.83 which - if valid - would reduce the
calculated resonant frequency to about 169 Hz or around E3.
As musical instruments are less than perfect Helmholtz spherical resonators, their resonant frequencies may be much less focussed allowing some
latitude 'on either side' of the calculated 'exact' resonant frequency where a range of sound hole diameters will give equally 'good' results. How
wide or narrow this range of tolerance might be would again have to be determined experimentally.
So, it will be interesting to see how the completed project oud with three sound holes will respond.
To clarify my thoughts and calculation procedures, I attach my notes for information.
Before resuming construction work on the project oud (early November) some preliminary thought will now be given to the tuning and fretting of the oud
based on the available historical evidence.
[file]11777[/file]
|
|
|
jdowning
Oud Junkie
    
Posts: 3485
Registered: 8-2-2006
Location: Ontario, Canada
Member Is Offline
Mood: No Mood
|
|
The study of the early Arabian and Persian theoretical works on music (with reference to the fretted oud) is a vast and complicated specialist subject
in its own right and there are many research papers - written by both Western and Eastern authorities and available for reference - for those with the
stamina to explore the fine detail.
As I have little detailed knowledge of the subject matter and not being in a position to examine primary source documentation, I must try to learn
something from the work of others who are expert in the field.
My perspective is that of a lute player but interested in the role that the oud has played historically in the development of the lute in Europe -
particularly as influenced by Moorish 'Spain'.
An interesting article that summarises the historical developments very well (in my opinion), from the Eastern perspective, is "The Arab Contribution
to Music of the Western World" by Dr. Rabah Saoud at:
http://www.muslimheritage.com
Dr Saoud highlights a number of interesting points. One is that, in some cases, the oud was played with the strings being struck - not with a risha or
plectrum - but with thumb and first finger in sequence - a device known as Jass (Al-Khindi 9th C) and later described in detail by Al- Khawarizimi
(10th C). So this precedes, by at least 7 centuries, the 'innovative' technique - introduced in the 16th C for the lute in Europe - evidence used to
support the claim that early polyphony (organum) in Europe was learned from the Moors - probably by the Europeans studying music at the Moorish
University of Cordoba.
More to follow!
|
|
|
patheslip
Oud Junkie
    
Posts: 160
Registered: 5-24-2008
Location: Welsh Marches
Member Is Offline
Mood: smooth
|
|
I just though that I ought to complicate matters, as the acoustics of ouds, lutes and guitars have proved to be so simple.
To add to the rosettes of oud and lute, tornovoz or tornavoz have been used in guitars, as well as the parchment roses from the baroque. There's a
whole world out there to investigate.
There does seem to be some consensus that rosettes increase the sustain, especially lower down the register (vis http://thamesclassicalguitars.com). This supports your experimental results.
I wonder whether the complexities of shape in oud, lute or guitar are such that Helmholtz has little to offer here.
Keep up the good work.
|
|
|
jdowning
Oud Junkie
    
Posts: 3485
Registered: 8-2-2006
Location: Ontario, Canada
Member Is Offline
Mood: No Mood
|
|
Thanks for your comments patheslip - nice guitars, although the powerful ' booming' bass, beloved of 'classical' guitar enthusiasts (thanks to
Helmholtz), is no longer to my taste.
The situation is indeed complex but I am still hoping that there might be a simplified approach in the application of the Helmholtz formula - but
admit that I could well be wrong in my optimism.
The complexity of the situation, I am sure, defies precise mathematical analysis - so it is up to the 'hands on' experimenters to try to pave a way
forward (if there is one). The problem is that few may be willing to devote the time necessary, not only to undertake this research work, but to then
to openly share the results of their efforts for the benefit of all.
|
|
|
jdowning
Oud Junkie
    
Posts: 3485
Registered: 8-2-2006
Location: Ontario, Canada
Member Is Offline
Mood: No Mood
|
|
The engraving, upon which the design of the project oud is based, is supposed to appear in an early 14th C copy of the Kitab al- Adwar by Safi al-Din
al-Urmawi - although this is yet to be positively confirmed.
A detailed analysis of the scale system developed by Safi al-Din can be found in the paper "Safi al-Din al-Urmawi and the Theory of Music" by Dr Fazil
Arsian published by the Foundation for Science Technology and Civilisation. Free for download and recommended reading for those interested at
http://www.muslimheritage.com
Dr H.G. Farmer in his paper "The Lute Scale of Avicenna" describes the historical development of the various scale systems for the oud from the
earliest times up to the theoretical works on music by Ibn Sina (otherwise known as Avicenna) in the 11th C.
He ends his article by stating that although the scale system developed by Avicenna was certainly an improvement on Al-Farabi's scale and tuning, it
was not until the time of Safi al-Din that an absolutely perfect scale was evolved.
The strings of a four course oud from bass to treble were named "Bamm', 'Mathlath', 'Mathna' and 'Zir'- tuned a fourth apart.
Although Ziryab was first to add a fifth string to the oud
(9th C Moorish 'Spain'), it was Al Kindi who first suggested adoption of this innovation throughout the East. Al Kindi called the fifth string 'zir
thani' but the name given to it by later writers was 'Hadd'. The 'Hadd' string was a treble string placed above the 'Zir' string (or below - depending
upon one's perspective!) and tuned in interval of a fourth higher.
The fifth string allowed the expansion of the tonal range of the oud to two octaves.
The various proposed theoretical placement of the frets, founded upon Pythagorean intervals, is complex (no wonder frets were eventually abandoned by
the oudists!) and, as I am currently still on a learning curve on this subject, am in no position to go into any detailed discussion about this or
that theoretical fret placement. In any case, oud players of the time did not use all of the fret positions dictated by theory but selected those that
suited the musical customs of a particular region, their personal preferences, best for a particular mode etc.
Dr Fazil Arsian describes, in schematic, the oud tablature used by Safi al-Din. As the number of frets (7) on the oud engraving matches the tablature
schematic this may be partial confirmation that the engraving is indeed part of the Kitab al-Adwar.
Dr Fazil Arsian's paper is published in English so he accordingly transcribes the original Arabic text into Roman (while referencing the original
Arabic). The attached image shows his transcribed tablature format overlaid on a tracing of the oud engraving.
For information and comparison an example of early German lute tablature is attached. This is from the book 'Utilis and Compendiara' by Hans
Judenkunig, dated 1523.
While everything is in reverse and upside down - note that the German tablature - although for a 6 course lute - was originally designed for a 5
course lute (open strings from bass to treble numbered 1 to 5). The additional 6th course in the bass requiring a new set of characters A, B, C ....
(This modification can also be found in the earliest examples of 16th 'French' tablature originally devised for a five course lute).
German tablature - the earliest example for the lute - was supposed to have been invented by blind organist Conrad Paumann - but was it? Or was this
just an adoption of 13th C oud tablature?
As an aside, I have always been intrigued by the name of the author of 'Utilis and Compendiara' which translates to 'King of the Jews'. Does this have
some, as yet, unexplained significance - a secret title, 'nom de plume' perhaps? But why?
More to follow.

|
|
|
jdowning
Oud Junkie
    
Posts: 3485
Registered: 8-2-2006
Location: Ontario, Canada
Member Is Offline
Mood: No Mood
|
|
In his paper "The Lute Scale of Avicenna", Dr H.G. Farmer observes a variation of the theoretical scale system proposed by Ibn Sina. This improvement
on the Al-Farabi scale was achieved tuning by tuning the 'Zir' string a major third from from the 'Mathna' string because "it embraced the elusive
Zalzalian notes in the second octave"
This is an interesting theoretical scale variation, as it relating (as it seems) to tuning of the Spanish Vihuela and early Guitar.
The early 4 course Guitar (in my opinion) is a 'cut down, low cost' version of the 6 course vihuela - eliminating the need for a (very expensive?)
treble string(s) and costly basses. Likewise for the 5 course vihuela.
The attached image is a comparative schematic of the relative tunings for information.
Next, a preliminary calculation and evaluation of string diameters (gauges) based upon historical evidence for oud strings made from silk and gut.

|
|
|
| Pages:
1
..
8
9
10
11
12
..
16 |